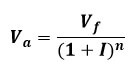Veíamos en la entrada sobre la inflación que el valor del dinero cambia con el paso del tiempo. Así, decíamos en el ejemplo que con una tasa de inflación del 5%, 1.000 euros equivaldrían a tan sólo 614 euros diez años más tarde.
Es por eso que no es muy inteligente aquello de dejar su dinero debajo del colchón, sino que es recomendable e incluso necesario invertirlo de alguna manera para al menos contrarrestar el efecto de la inflación, ya que si no lo hacemos el valor de nuestro dinero tiende a desaparecer.
Vamos a suponer que disponemos de 1.000 euros y decidimos invertirlos a plazo fijo con un interés del 5%. Veamos cómo aumenta nuestro dinero con el paso del tiempo:
Lo que estamos haciendo es simplemente multiplicar cada año por 1,05 (uno más la tasa de interés). Como vemos, dentro de diez años tendremos 1.629 €. Esto parece un buen negocio a simple vista, ya que hemos aumentado considerablemente la cantidad de dinero, pero tal y como vimos en la entrada referida al principio, debemos considerar también la inflación. En la siguiente tabla calculamos el valor actual de nuestros ahorros, dividiendo la cantidad por 1,05 (uno más la inflación) el número de veces igual a los años transcurridos. Es decir, los 1.276 euros del quinto año los dividiremos cinco veces por 1,05 para saber a cuánto dinero de hoy equivaldrían. El resultado es el siguiente:
La explicación es sencilla: la tasa de interés del 5% es igual a la inflación, con lo cual el aumento de nuestro capital simplemente neutraliza la depreciación del mismo con el paso del tiempo. Esta es entonces la situación en la que nuestro dinero no pierde valor, pero tampoco gana a pesar de estar invertido con una tasa de interés. Así pues, solamente si logramos invertir nuestro dinero con una tasa mayor a la inflación estaremos ganando realmente poder adquisitivo. Si por el contrario nuestra inversión rentabiliza por debajo de la inflación, entonces estaremos perdiendo capacidad adquisitiva a pesar de que cada vez tengamos más dinero disponible, al contrario de lo que nuestra lógica nos indica en un primer momento.
Veamos para acabar las dos fórmulas utilizadas en la tabla anterior:
Dinero ahorrado (inversión)
Dinero final = Dinero inicial * (1 + Interés) ^ (número de años)
Valor actual (inflación)
Valor actual = Valor en unos años / (1 + Inflación) ^ (número de años)
Como bien podrás observar las dos fórmulas anteriores son en realidad la misma, pero es importante que no memorices la fórmula sino que entiendas e interiorices los conceptos explicados en las dos últimas entradas ya que son la base para muchos cálculos y conceptos futuros. Por lo tanto te invitamos a dejar tus dudas en los comentarios en caso de que algo no haya quedado suficientemente claro.