Six Sigma, también escrito 6σ es una metodología de mejora de procesos creada por Bill Smith en Motorola e implementada en dicha compañía en 1988, aunque especialmente General Electric fue la encargada de popularizarla.
El nombre Six Sigma tiene su origen en la estadística y define el objetivo de los fallos permitidos en un proceso de fabricación. En este artículo explicamos con detalle el origen estadístico del nombre.
La distribución normal o campana de Gauss
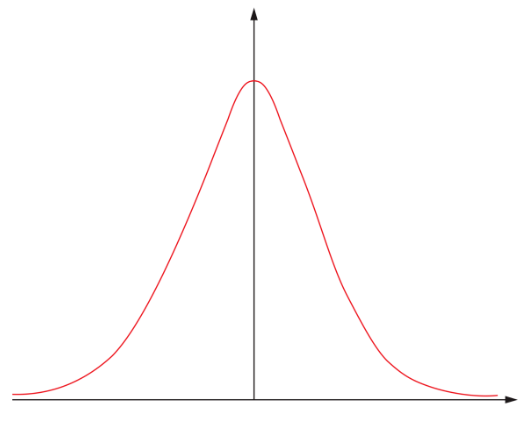
Generalmente decimos que las mediciones en un proceso de fabricación tienen una distribución normal, también conocida como campana de Gauss. La mayoría de los valores se encuentran próximos a la media, mientras que cuanto más nos alejamos de dicha media más improbable es que obtengamos resultados de medición. La gráfica inferior muestra una distribución normal típica. El eje vertical sería el número de resultados y el eje horizontal el resultado de la medición.
Tal y como explicábamos anteriormente, la gráfica muestra que el número de resultados entorno a la media (el centro del eje horizontal) es muy elevado, mientras que el número de muestras con valores alejados de la media decrece rápidamente.
Desviación típica Sigma (σ)
La letra griega Sigma (σ) se utiliza para definir la desviación estándar de un conjunto de mediciones, y nos da una idea de la anchura de la curva de Gauss que obtendríamos al medir todas nuestras piezas fabricadas. Sigma se calcula de la siguiente forma:
n = número de mediciones
xi = resultado de cada una de las mediciones
µ = media de todas las mediciones (igual al objetivo de fabricación)
Dicho de otro modo, la desviación estándar (también llamada desviación típica) se obtiene de calcular la suma de todos los errores al cuadrado, dividir dicha suma entre el número de mediciones y aplicar la raíz cuadrada al resultado.
La interpretación gráfica de la desviación estándar es que cuanto mayor sea su valor, más ancha será la curva de distribución.
Número de defectos
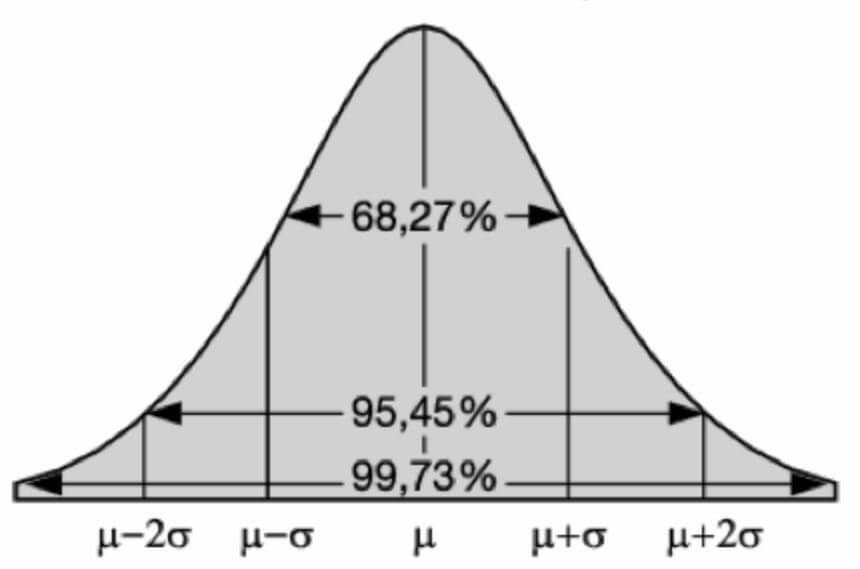
Una de las propiedades de la distribución normal o gaussiana es que podemos calcular el número de mediciones que se encontrarán dentro de unos valores comprendidos entre un número determinado de desviaciones típicas. El resultado es independiente tanto de la media como del propio valor de la desviación, y siempre nos dará el siguiente resultado:
- Valores entre (µ-σ) y (µ+σ) = 68,27 %
- Valores entre (µ-2σ) y (µ+2σ) = 95,45 %
- Valores entre (µ-3σ) y (µ+3σ) = 99,73 %
De manera inversa a lo anterior podremos calcular el número de defectos que seguramente se producirán en nuestra fabricación. Imaginemos que producimos barras de hierro que deben medir 25mm. Comenzamos a producir y a hacer mediciones de los resultados, tras lo que calculamos que nuestro proceso de fabricación resulta en una desviación típica de 1mm. Esta desviación típica la calcularíamos utilizando la fórmula del apartado anterior para un alto número de muestras.
La desviación típica de 1mm significa que un 68,27% de las piezas medirán entre 24 y 26mm (media +/- una desviación típica) o lo que es lo mismo, un 31,73% medirán menos de 24mm o más de 26mm.
Si ahora imaginamos que precisamente hemos definido con nuestro cliente una tolerancia admisible de +/- 1mm entonces sin duda deberíamos mejorar nuestro proceso de fabricación, puesto que no nos podemos permitir desechar un 31,73% de las piezas. Si logramos optimizar dicho proceso hasta obtener una desviación estándar de 0,33mm, entonces los +/- 1mm requeridos por el cliente pasarían a significar +/- 3σ, con lo que ahora el 99,73% de las piezas fabricadas estarían dentro de los límites aceptables. Esto significaría pasar a tener un porcentaje de error de tan sólo 0,27%. Estaríamos en este caso hablando de un proceso con calidad tres Sigma, 3σ.
El desplazamiento de 1,5 sigma
Llegado este punto, seguro que intuyes ya que 6σ se utilizará entonces para denominar un proceso mediante el cual producimos piezas cuyos límites de aceptación se encuentran en +/- seis veces la desviación típica. Pues bien, en realidad esto no es del todo cierto.
Más arriba dimos los porcentajes de acierto para uno, dos y tres Sigma. En la distribución normal en total un 99,9999998% de los resultados se encuentran entre (µ-6σ) y (µ+6σ). Dicho de otra manera, podemos esperar que solamente 2 piezas de entre un billón se encuentren fuera de los límites de tolerancia.
Sin embargo, en la bibliografía siempre se habla de 3,4 defectos por millón de eventos u oportunidades (DPMO) cuando nos referimos a 6σ en lugar de los 2 defectos por billón mencionados en el párrafo anterior. Esto es debido a la introducción del desplazamiento de 1,5 sigma.
Una vez medido un proceso de fabricación y obtenida por tanto su distribución normal y su desviación típica, es aceptado comúnmente que a lo largo del tiempo el proceso completo acabará teniendo una desviación adicional de +/- 1,5σ. Esto es equivalente a mover la curva de distribución una distancia de 1,5σ a ambos lados del centro. Cuando consideramos esto, el punto que inicialmente se correspondería con 6σ ahora es el 4,5σ de la curva de distribución de la derecha, mientras que el punto -6σ pasa a ser el -4,5σ de la curva de distribución de la izquierda.
Por lo tanto, cuando consideramos el desplazamiento de 1,5σ, el valor de los defectos por millón (DPMO) pasan de ser los correspondientes a 6σ (en el caso de una única curva centrada en la media) a ser los correspondientes a 4,5σ. Por eso en Six Sigma hablamos de 3,4 DPMO.
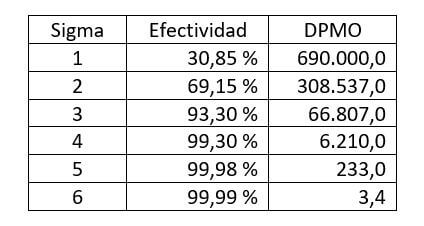
A continuación vemos los valores de efectividad (porcentaje de resultados válidos) y el número de DPMO para los diferentes niveles de sigma una vez aplicado el desplazamiento de 1,5σ.
Conclusión
Este artículo nos aporta la base de estadística necesaria para entender lo que son la distribución normal, la desviación típica y los porcentajes de error (DPMO) asociados a las imperfecciones en la fabricación. Dicha teoría es el punto de partida para la mejora de calidad y el proceso Six Sigma que veremos en un artículo posterior.


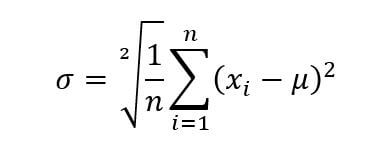



hola necesito informacion: experimento fisico o simulacion
Hola Elba,
no entiendo la pregunta, podrías ser más específica?